în aproape toate exemplele de coduri pe care le-am văzut despre un VAE, funcțiile de pierdere sunt definite după cum urmează (acesta este codul tensorflow, dar am văzut similar pentru theano, torță etc. Este, de asemenea, pentru un convnet, dar acest lucru nu este prea relevant, afectează doar axele care sunt preluate sumele):
Cu toate acestea, intervalul numeric kl_loss și rec_loss sunt foarte dependenți de intensitățile latente ale spațiului și de dimensiunea caracteristicii de intrare (de exemplu, rezoluția pixelilor). Ar fi rezonabil să înlocuiți sumele reduce_sum cu reduce_mean pentru a obține KLD z-dim și per pixel (sau caracteristică) LSE sau BCE? Mai important, cum ponderăm pierderea latentă cu pierderea din reconstrucție atunci când însumăm pentru pierderea finală? Este doar o încercare și o eroare? sau există vreo teorie (sau cel puțin o regulă generală) pentru aceasta? Nu am putut găsi nicio informație despre asta nicăieri (inclusiv hârtia originală).
Problema pe care o am este că, dacă echilibrul dintre dimensiunile caracteristicii mele de intrare (x) și dimensiunile spațiului latent (z) nu este „optim”, fie reconstituirile mele sunt foarte bune, dar spațiul latent învățat este nestructurat (dacă dimensiunile x este foarte mare și eroarea de reconstrucție domină peste KLD), sau invers (reconstrucțiile nu sunt bune, dar spațiul latent învățat este bine structurat dacă KLD domină).
Trebuie să normalizez pierderea de reconstrucție (împărțirea la dimensiunea caracteristicii de intrare) și KLD (împărțirea la dimensiunile z) și apoi ponderarea manuală a termenului KLD cu un factor de greutate arbitrar (normalizarea este astfel încât să pot folosi același sau greutate similară independentă de dimensiunile lui x sau z). Empiric, am găsit în jur de 0,1 pentru a oferi un echilibru bun între reconstrucție și spațiul latent structurat, care se simte ca un „punct dulce” pentru mine. Caut lucrări prealabile în acest domeniu.
La cerere, notația matematică de mai sus (concentrându-se pe pierderea L2 pentru eroare de reconstrucție)
unde $ J $ este dimensionalitatea vectorului latent $ z $ (și media corespunzătoare $ \ mu $ și varianța $ \ sigma ^ 2 $), $ K $ este dimensionalitatea caracteristicilor de intrare, $ M $ este mini-lotul dimensiunea, indicativul $ (i) $ denotă $ i $ th punctul de date și $ \ mathcal ^ $ este pierderea pentru $ m $ th mini-lot.
4 Răspunsuri 4
Pentru oricine se poticnește în această postare și caută un răspuns, acest fir de twitter a adăugat o mulțime de informații foarte utile.
discută întrebarea mea exactă cu câteva experimente. Interesant, se pare că $ \ beta_ $ (care este similar cu greutatea mea normală KLD) este, de asemenea, centrat în jurul valorii de 0,1, cu valori mai mari care oferă spațiu latent mai structurat cu prețul unei reconstrucții mai slabe și valori mai mici, oferind o reconstrucție mai bună cu spațiu latent mai puțin structurat (deși se concentrează în mod special pe învățarea reprezentărilor despărțite).
și lectură conexă (unde sunt discutate probleme similare)
Aș dori să mai adaug o lucrare legată de această problemă (nu pot să comentez din cauza reputației mele scăzute în acest moment).
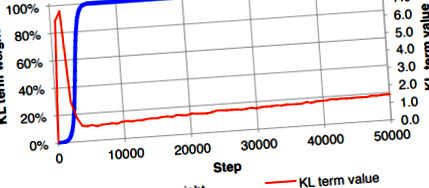
În subsecțiunea 3.1 a lucrării, autorii au specificat că nu au reușit să instruiască o implementare directă a VAE care a egalizat în mod egal probabilitatea și divergența KL. În cazul lor, pierderea KL a fost redusă nedorit la zero, deși se aștepta să aibă o valoare mică. Pentru a depăși acest lucru, au propus să utilizeze „recocirea costurilor KL”, care a crescut încet factorul de greutate al termenului de divergență KL (curba albastră) de la 0 la 1.
Această soluție de rezolvare este aplicată și în Ladder VAE.
Bowman, S.R., Vilnis, L., Vinyals, O., Dai, A.M., Jozefowicz, R. și Bengio, S., 2015. Generarea de propoziții dintr-un spațiu continuu. arXiv preprint arXiv: 1511.06349.
Actualizare în dec. 6 2020: am făcut o postare pe blog pentru a explica acest lucru în detalii.
În cele din urmă reușesc să dau seama de motivul ponderării divergenței KL în VAE. Este vorba mai mult despre constanta normalizată a distribuției modelate pentru variabila țintă. Aici, voi prezenta câteva distribuții de ieșire pe care le folosim adesea. Cea mai mare parte a notației va urma cartea „Recunoașterea modelelor și învățarea automată”.
- Regresie liniară (regresie nelimitată): (secțiunea 3.1.1 la pagina 140) - Acest lucru explică diferența de ponderare KL atunci când se utilizează pierderea MSE
Variabila țintă $ t $ se presupune că este suma funcției deterministe $ y (\ mathbf, \ mathbf) $ și un zgomot gaussian: \ begin t = y (\ mathbf, \ mathbf) + \ epsilon, \ qquad \ epsilon \ sim \ mathcal \ left (\ epsilon | 0, \ color ^ \ right) \ end Variabila țintă este, prin urmare, modelată ca o variabilă aleatorie Gaussiană, cu log-probabilitatea dată astfel: \ begin p (t | \ mathbf, \ mathbf, \ color) = \ mathcal \ left (t | y (\ mathbf, \ mathbf), \ color ^ \ right) \ end Având în vedere această presupunere, probabilitatea jurnalului la punctele de date $ \ _, t _ \> _ ^ $ este: \ begin \ ln p (\ mathbf | \ mathbf, \ mathbf, \ color) = \ frac \ ln \ frac> - \ color E _ (\ mathbf), \ end unde: \ begin E _ (\ mathbf) = \ frac \ sum_ ^ [t_ - y (\ mathbf, \ mathbf)] ^. \ end Optimizăm adesea doar $ E _ (\ mathbf) $, nu întreaga probabilitate a jurnalului $ \ ln p (\ mathbf | \ mathbf, \ mathbf, \ beta) $, rezultând ignorarea preciziei $ \ color $. Acest lucru ar putea fi în regulă pentru regresia convențională în care pierderea constă doar în log-probabilitatea negativă (NLL) $ - \ ln p (\ mathbf | \ mathbf, \ mathbf, \ beta) $, iar predicția ar fi media variabilă țintă $ t $ .
Cu toate acestea, pierderea în VAE constă în NLL (sau pierderea reconstrucției) și regularizarea (pierderea KL). Prin urmare, dacă factorul de greutate al termenului MSE (sau, $ E _ (\ mathbf) $ în acest caz) este 1, trebuie să ponderăm divergența KL cu un factor $ \ beta_ = 1/\ color $ pentru a fi corect matematic . În practică, oamenii găsesc adesea o valoare bună a preciziei $ \ beta_ $ prin reglarea hiper-parametrilor. O altă abordare este de a învăța $ \ color $ considerându-l ca un parametru care poate fi învățat, care se obține prin minimizarea întregii funcții de pierdere VAE.
- Regresie logistică - Acest lucru explică cazul pierderii binare a entropiei încrucișate utilizate pentru imaginile alb-negru
Să luăm în considerare cazul clasificării binare. Adevărul de bază este fie 0, fie 1, iar variabila țintă $ t = p (y = 1 | \ mathbf) $ se presupune că urmează o distribuție Bernoulli: \ begin p (t | \ mathbf, \ mathbf) = \ mathcal(t | y (\ mathbf, \ mathbf)) = \ left [y (\ mathbf, \ mathbf) \ right] ^ \ left [1 - y (\ mathbf, \ mathbf) \ right) ^. \ end Prin urmare, NLL în acest caz este dată de: \ begin - \ ln p (t | \ mathbf, \ mathbf) = - \ left [t \ ln y (\ mathbf, \ mathbf) + (1 - t) \ ln (1 - y (\ mathbf, \ mathbf)) \ right], \ end care este pierderea binară de entropie încrucișată. (Se poate extinde la softmax pentru clasificarea multiclass utilizând o distribuție categorică pentru a duce la pierderea entropiei încrucișate.)
Pentru setul de date MNIST (sau imagini alb-negru), fiecare pixel este 0 sau 1 și, prin urmare, putem folosi pierderea binară de entropie încrucișată ca pierdere de reconstrucție în VAE pentru a prezice probabilitatea ca valoarea unui pixel să fie 1 Și întrucât media distribuției Bernoulli este egală cu $ y (\ mathbf, \ mathbf) $, folosim adesea $ y (\ mathbf, \ mathbf) $ ca intensitate a pixelilor pentru a trasa imaginile reconstituite.
Rețineți că atunci când se utilizează pierderea binară de entropie încrucișată într-un VAE pentru imagini alb-negru, nu este necesar să ponderăm termenul de divergență KL, care a fost văzut în multe implementări.
- Regresie limitată (de exemplu, regresie în [0, 1]) - Acest lucru explică cazul ponderării divergenței KL atunci când se utilizează pierderea binară de entropie încrucișată pentru imaginile color
După cum sa explicat în regresia logistică, suportul (sau eticheta) unei distribuții Bernoulli este $ \ $, nu $ [0, 1] $, dar în practică, este încă folosit pentru reconstrucția imaginii color, care necesită un suport în $ [0, 1] $ sau $ \ $ .
Deoarece interesul nostru este cazul asistenței în $ [0, 1] $, am putea găsi o distribuție continuă care are suport în $ [0, 1] $ pentru a ne modela predicția. Una simplă este distribuția beta. În acest caz, predicția noastră ar fi cei 2 parametri $ \ alpha $ și $ \ beta $. Pare complicat?
Din fericire, a fost propusă recent o versiune continuă a distribuției Bernoulli, astfel încât, putem folosi în continuare pierderea binară de entropie încrucișată pentru a prezice intensitatea unui pixel cu unele modificări minime. Vă rugăm să consultați lucrarea „Distribuția continuă Bernoulli: remedierea unei erori omniprezente în VAE” sau pagina Wikipedia pentru detalii suplimentare despre distribuție.
În ipoteza distribuției Bernoulli continue, probabilitatea logului poate fi exprimată ca: \ begin \ ln p (t | \ mathbf, \ mathbf) = \ mathcal (t | y (\ mathbf, \ mathbf)) = C ( y (\ mathbf, \ mathbf)) (y (\ mathbf, \ mathbf)) ^ (1 - y (\ mathbf, \ mathbf)) ^, \ end unde $ C (y (\ mathbf, \ mathbf)) $ este constanta normalizata.
Prin urmare, atunci când lucrăm cu VAE care implică pierderea binară de entropie încrucișată, în loc să reglăm pentru un factor de greutate al termenului KL - care ar putea fi matematic incorect, adăugăm pur și simplu $ - \ ln C (y (\ mathbf, \ mathbf)) $ în pierdere și apoi optimizează.
- Învățare automată - Rețea neuronală; Reducerea greutății - validat încrucișat
- Funcția de pierdere Funcția de pierdere în învățarea automată
- Avocat; Pierderea în greutate uimitoare a 14 PIETRE după renunțarea la băuturi gaze și învățarea de a găti
- Sistem multifuncțional Mașină de crioterapie Mașină de înfrumusețare pentru slăbire a grăsimilor - China
- Masaj centura masina de slăbit x5 arderea grăsimilor slăbire leneș slăbire încărcare vibrații infraroșu